
This includes elimination, substitution, the quadratic formula, Cramer's rule and many more. As a result, Wolfram|Alpha also has separate algorithms to show algebraic operations step by step using classic techniques that are easy for humans to recognize and follow. These methods are carefully designed and chosen to enable Wolfram|Alpha to solve the greatest variety of problems while also minimizing computation time.Īlthough such methods are useful for direct solutions, it is also important for the system to understand how a human would solve the same problem. Other operations rely on theorems and algorithms from number theory, abstract algebra and other advanced fields to compute results. In some cases, linear algebra methods such as Gaussian elimination are used, with optimizations to increase speed and reliability. How Wolfram|Alpha solves equationsįor equation solving, Wolfram|Alpha calls the Wolfram Language's Solve and Reduce functions, which contain a broad range of methods for all kinds of algebra, from basic linear and quadratic equations to multivariate nonlinear systems. Similar remarks hold for working with systems of inequalities: the linear case can be handled using methods covered in linear algebra courses, whereas higher-degree polynomial systems typically require more sophisticated computational tools.
More advanced methods are needed to find roots of simultaneous systems of nonlinear equations. This too is typically encountered in secondary or college math curricula. It will also calculate the roots of the polynomials and factor them. Systems of linear equations are often solved using Gaussian elimination or related methods. The calculator will find (with steps shown) the sum, difference, product, and result of the division of two polynomials (quadratic, binomial, trinomial, etc.). These use methods from complex analysis as well as sophisticated numerical algorithms, and indeed, this is an area of ongoing research and development. There are more advanced formulas for expressing roots of cubic and quartic polynomials, and also a number of numeric methods for approximating roots of arbitrary polynomials.
#Polynomial equation maker how to#
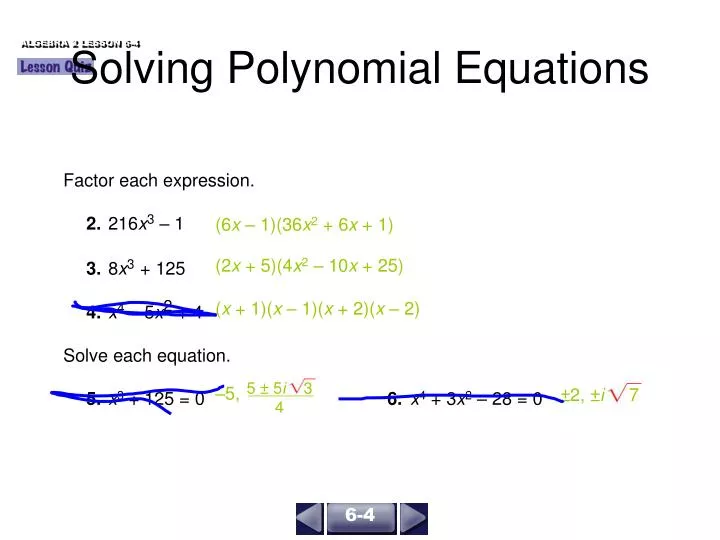
One also learns how to find roots of all quadratic polynomials, using square roots (arising from the discriminant) when necessary. One learns about the "factor theorem," typically in a second course on algebra, as a way to find all roots that are rational numbers. This polynomial is considered to have two roots, both equal to 3. To understand what is meant by multiplicity, take, for example. If has degree, then it is well known that there are roots, once one takes into account multiplicity. The largest exponent of appearing in is called the degree of. Partial Fraction Decomposition CalculatorĪbout solving equations A value is said to be a root of a polynomial if.
#Polynomial equation maker generator#
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator Here are some examples illustrating how to formulate queries. To avoid ambiguous queries, make sure to use parentheses where necessary. It also factors polynomials, plots polynomial solution sets and inequalities and more.Įnter your queries using plain English. Note that the quadratic formula actually has many real-world applications, such as calculating areas, projectile trajectories, and speed, among others.Wolfram|Alpha is a great tool for finding polynomial roots and solving systems of equations. This is demonstrated by the graph provided below. Furthermore, the quadratic formula also provides the axis of symmetry of the parabola. The x values found through the quadratic formula are roots of the quadratic equation that represent the x values where any parabola crosses the x-axis. Recall that the ± exists as a function of computing a square root, making both positive and negative roots solutions of the quadratic equation. Below is the quadratic formula, as well as its derivation.įrom this point, it is possible to complete the square using the relationship that:Ĭontinuing the derivation using this relationship: Only the use of the quadratic formula, as well as the basics of completing the square, will be discussed here (since the derivation of the formula involves completing the square).


A quadratic equation can be solved in multiple ways, including factoring, using the quadratic formula, completing the square, or graphing. For example, a cannot be 0, or the equation would be linear rather than quadratic. The numerals a, b, and c are coefficients of the equation, and they represent known numbers. Where x is an unknown, a is referred to as the quadratic coefficient, b the linear coefficient, and c the constant. In algebra, a quadratic equation is any polynomial equation of the second degree with the following form:

Fractional values such as 3/4 can be used.


 0 kommentar(er)
0 kommentar(er)
